Chryzode
Un voyage en images dans la science des nombres (arithmétique)
A pictorial travel into arithmetic

Des chryzodes en lignes aux chryzodes en points d'intersection

 
En tentant d'illustrer les aspects à la fois corpusculaires et ondulatoires de la matière, il est astucieux de ne faire apparaître (grâce à l'informatique) que les points de croisement des lignes (> voir chryzodes en lignes).
Nous faisons alors de nouvelles découvertes et le chryzode en points d'intersection prend un relief inédit. 

  

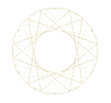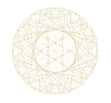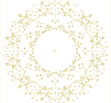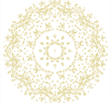
<-- Multiplication par 3 dans un cercle partagé en 211 points equidistants

EXEMPLE 3 /
Multiplication par 3 en points d'intersection dans un cercle partagé en 1401 points equidistants

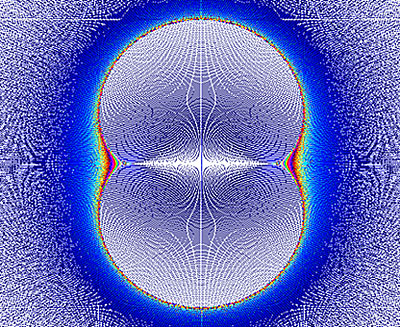
Multiplication par 3 en points d'intersection
dans un cercle partagé en 1401 points equidistants

.
.

Dans la courbe en forme de huit, nous découvrons de multiples courbes à la facon de certains moirages.
Ici les chryzodes nous permettent de visualiser les partiels d'une onde.

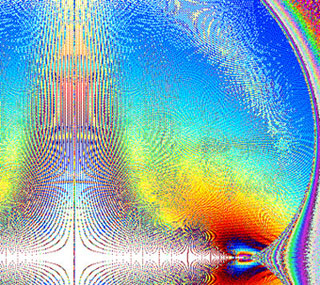
détail dans des cercles partagés de 1401 à 1441 points

EXEMPLE 4 / MULTIPLICATION PAR 3 DANS LES NOMBRES MULTIPLES DE 7 

Nous représentons la multiplication par 3 sur des cercles multiples de 7 (les points d'intersection de la mult. par 3 dans un cercle de 7 points auxquels on superpose ceux dans un cercle de 14 points, puis de 21 points, etc.). Cette fois, dans la courbe en forme de huit, nous découvrons de multiples «tops» de synchronisation organisés en faisceaux. Ces faisceaux illustrent les harmoniques du système.

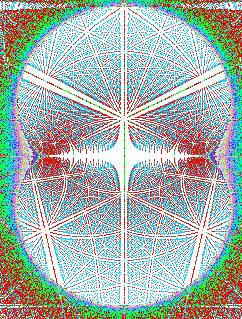
Multiplication par 3 en points d'intersection
dans un cercle partagé en 7, 14, 21, 28, etc. points (multiples de 7)

construction du chryzode

EXEMPLE 5
AGRANDISSEMENT DE LA MULTIPLICATION PAR 3 DANS LES NOMBRES MULTIPLES DE 7 

.
.

Notons que si nous agrandissons le dessin, nous ne retrouvons pas la courbe du départ. 
Les chryzodes ne sont donc pas de la famille des fractales.
Par contre, ils illustrent bien les relations d'harmonie qui peuvent exister au sein d'un ensemble de phénomènes périodiques.  Sous cet angle de vue, ils nous enseignent surtout une science de l'harmonie et du relationel. A bon entendeur !