Chryzode
Un voyage en images dans la science des nombres (arithmétique)
A pictorial travel into arithmetic
Cybernétique Cognitive
Annexe de la thèse de doctorat de Pierre Germain "Relations entre l'architecture des réseaux de neurones naturels, le codage en population et l'apprentissage" - Université Paris 6 - 1997
D-1- De nouveaux modèles pour représenter un ensemble de neurones en interaction.Parmi les obstacles rencontrés par l'expérimentateur lors de sa recherche, reconnaissons au moins 3 aspects essentiels qu'il va nous falloir recomposer comme les pièces d'un puzzle. .
3)- Discrétisation de l'information . D-2- Réseau circulaireFace à ces difficultés, l'idée nouvelle à l'origine du système de représentation des chryzodes réside dans l'utilisation d'un CERCLE, d'un ANNEAU, étalonné comme une HORLOGE, et dans lequel nous représentons par des lignes, les chemins, les circuits entre un ensemble d'éléments en interaction.
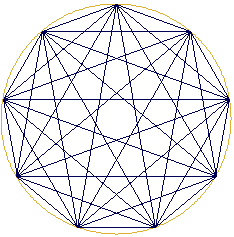
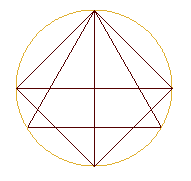
Cette particularité arithmétique, nous permet d'étudier le modèle à partir des lois régissant le domaine des nombres. La voie est tentante, car de la mécanique quantique à la perception des harmoniques d'un violon, les propriétés arithmétiques jouent un rôle fondamental. . D-3- Superpositions des polygones étoilés de différents modulesMaintenant en une deuxième étape nous allons superposer dans une même figure des modules disposant d'un nombre croissant d'éléments, soit la suite des entiers 2, 3, 4, etc. Ainsi, sur le cercle, pour représenter le nombre 2, nous déterminons un point origine, puis nous plaçons un deuxième point que nous relions par un trait au point origine.
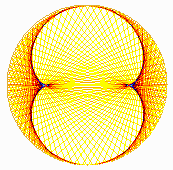
De façon plus drastique, nous constatons que la superposition
des réseaux met en évidence une série d'enveloppes
hypocycloïdiques (internes au cercle). En prolongeant les lignes hors
du cercle, nous aurions également observé la présence
de courbes épicycloïdiques (externes au cercles).
L'instrument permet de réaliser et de découvrir d'innombrables figures inédites à ce jour. Aussi, l'équipe de recherche avec laquelle je travaille sur le sujet propose que l'on qualifie ces graphes du nom de Chryzode (1987). Ce mot "chryzode" est déduit de "chryzos" (écriture en or) et de "zooïde" (cercle). Il signifierait une écriture en or sur un cercle. Pour nous, il désigne la grande famille de formes issues de la représentation des nombres au moyen de vecteurs (et d'intersections de ces vecteurs) inscrits sur une circonférence graduée. . D-4- Première étape : L'ECHAFAUDAGERevenons à notre dernier exemple pour constater que l'extrême enchevêtrement du réseau suggère une articulation sous-jacente. Pour cet effet, l'application des suites arithmétiques au système en fait émerger comme un espèce d'alphabet de base. Son maniement permet de découvrir un monde foisonnant à peine exploré. Il nous renseigne aussi sur les structures, les résonances, les harmonies et les harmoniques des systèmes ondulatoires. Discernons y pour commencer au moins deux étapes fondamentales
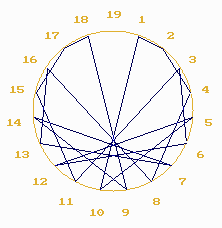
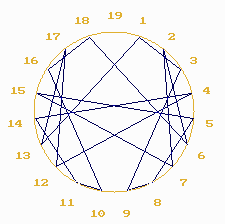
: l'échafaudage et les points d'intersections. Multiplication par 2 dans le nombre 19 Nous appelons ce nombre m "cercle-module m" ou "référentiel circulaire de valeur m". plus simplement nous dirons qu'il représente le modulo m. Dans l'exemple ci-dessous nous avons m= 19. Pour dessiner cette suite des doubles, nous nous aidons d'une circonférence
sur laquelle nous avons au préalable défini m points
équidistants numérotés de 1 à m.
En analysant un peu plus le processus nous remarquons qu'à
partir du 18ème terme la suite est devenue périodique
et nous nous retrouvons au point de départ. En arithmétique nous disons que 2 est l'inverse de 10 dans
le module 19. Dans une extrapolation musicale, l'on dirait que par le nombre 19, les harmonies de 2 se transforment en harmonies de 10. Sous cet angle de vue, les chryzodes paraîtraient être comme une représentation, une image de cette transformation ou harmonisation verse-inverse.
Multiplication par 3 dans le nombre 19
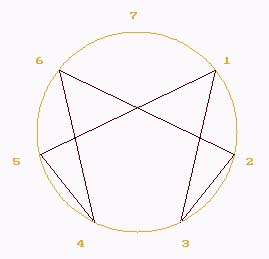
On constate alors que pour la multiplication par 3, les droites
sont toutes tangentes à une autre courbe cycloïdale. Celle-ci
en forme de huit est appelée "néphroïde". . D-5- Deuxième étape : LES POINTS D'INTERSECTIONQuand nous représentons de grandes séries de nombres, le graphe en ligne se surcharge et n'est plus guère exploitable. D'autre part, si nous voulons illustrer le discontinu, l'aspect corpusculaire du système, il est astucieux de faire apparaître uniquement les points d'intersection des vecteurs du chryzode en lignes et ceci grâce à l'ordinateur.
D-6- Superposition harmonique de réseauxEn poursuivant nos investigations nous constatons que les détails des formes issues de la multiplication par 3 dépendent de la valeur des nombres dans lesquels on la représente.
D-7-1-Des faisceaux de synchronisation au niveau des moléculesDans le cadre d'une approche cognitive, la découverte et la modélisation de faisceaux de synchronisation par superposition de réseaux méritent toute notre attention. En effet, nous avons là comme un pont pour mieux comprendre les propriétés des réseaux d'interconnexions du cerveau.
D-8- Le faisceau de synchronisation envisagé comme brique d'une gestion cognitive et comportementaleEn règle générale, avec le système des chryzodes, nous retrouvons les faisceaux de synchronisation dans toutes les superpositions harmoniques de réseaux de points. L'apparition de ces faisceaux dans les chryzodes et dans les radio-cristallographies
met la puce à l'oreille. D'autant que notre perception du visible
ne nous a pas habitués à un tel type de structure alors
qu'ils apparaissent assez rapidement dans la superposition de réseaux
de points (voir appendice 3). Probablement que s'ils ne sont pas visibles
directement à l'oeil nu, c'est que notre perception visible
ne couvre qu'une gamme de fréquence (du rouge à l'ultra-violet,
il n'y a qu'une multiplication par 2). Or, l'émergence des
faisceaux est liée à une croissance harmonique des fréquences
(ex: 2, , 8, 16, etc.). Extrapoler et poursuivre vers les mécanismes de la cognition est une aventure spéculative qui peut nous faire avancer de quelques étapes. Cependant, et l'on s'en rend vite compte, la tâche est colossale. Le domaine des nombres est infini, les formes que nous inventorions sont elles aussi infinies. Quant à l'outil mathématique classique, il se révèle incomplet pour cerner l'ensemble des possibilités. Il nous faudrait une super-fonction de Fourier, et la démarche actuelle vers les corrélations par ondelettes et les fonctions de Gabor vont dans ce sens. En ce qui concerne les chryzodes, tout reste à faire, si l'on fait omission des pistes que nous ont laissées Fermat, Pascal, Gauss et Poincaré. L'apport des chryzodes rend vraisemblable et envisageable de nouvelles hypothèses. Par exemple lors d'une analyse cognitive, le système met en place des sortes d'aiguilles, d'axes, ou de réseaux d'axes qui prennent leur origine dans les synchronisations issues de la superposition des différents niveaux de traitement d'une information. Ceci peut l'être autant par un effet excitateur des extrémités axonales que par un effet inhibiteur. Les faisceaux peuvent être isolés et fugaces comme dans le cas d'une petite excitation sensorielle ou plus intense, plus dense, comme dans le cas d'une concentration ou d'une méditation philosophique. Ce qui compte pour nous, c'est que ces vecteurs, un peu comme des chemins, des traits de mémoire, des "tubes" provenant des synchronisations entre les différentes couches opérant une analyse, puissent être utilisés instantanément ou ultérieurement (sommeil paradoxal) dans un ensemble architectural plus vaste. Nous aurions alors une sorte de gestion des "patterns", dans le sens défini par Jung, des moules, en quelque sorte un vocabulaire et une grammaire de la cognition. La difficulté est que, dans ce genre d'investigation, il est assez difficile de passer directement à l'expérimentation à cause d'aspects liés à la déontologie. Plus la faculté que nous souhaitons comprendre est élevée dans l'échelle des perceptions, plus il nous faut nous diriger vers les analystes, les philosophes, les visionnaires afin de décrypter leurs expériences à la lumière de notre foi investigatrice. En effet, les expériences à court terme sont difficilement envisageables et les recherches longues et pas toujours évidentes. Par exemple, avant d'obtenir un chryzode ressemblant au Rubisco, il nous a fallu analyser le processus mis en place dans une radio-cristallographie pour y constater que l'appareillage produisait une inversion homologique. D'un autre côté, alors qu'un biologiste nous conseillait de présenter les images issues des chryzodes à des déficients mentaux légers afin d'étudier leur réactions, certains mathématiciens en place élevèrent un tollé quand nous leur avons soumis cette proposition d'expérimentation. Il nous a paru alors utile d'éviter une démarche conflictuelle. En progressant dans notre recherche sur les chryzodes nous avons trouvé de multiples pistes, les corrélations avec les faisceaux de synchronisation n'est que celle qui nous semble la plus consistante. D'autres voies sont à même de nous laisser quelques chances d'avancer un peu. Nous présentons dans l'appendice celles qui nous semblent les plus prometteuses. Un travail immense reste à faire. Et bien que les chryzodes semblent en ce moment soulever plus de questions qu'ils n'en résolvent, ils ont au moins l'avantage de nous offrir des sens nouveaux pour ce qui nous avait apparu jusqu'alors être un labyrinthe de complexité. . D-9- Un peu d'épistémologieRetenons donc, les chryzodes permettent d'explorer toutes les fonctions opérant sur les nombres entiers et par approximation sur les réels. Qu'il s'agisse des décimales d'une fraction périodique ou d'une équation compliquée, ils mettent toujours en relief des propriétés que cache l'abrupte austérité d'un formalisme intégro-différentiel. C'est une nouvelle façon de représenter certains objets mathématiques, tels des réseaux de lignes ou de points, de visualiser des abstractions logiques, de manipuler une sorte d'alphabet des figures. Vue la richesse des résultats esthétiques et rationnels obtenus, le système paraît se situer à un carrefour épistémologique et semble capable de générer un ensemble de sens possibles. Ceux-ci peuvent alimenter l'imagination et la créativité de tous, tant dans le domaine de la recherche que dans le domaine de l'expérimentation et celui en pleine expansion de la modélisation. Notons, tout d'abord, qu'à partir d'un mécanisme arithmético-géométrique simple on obtient de l'harmonie, de l'organisation, mais ni désordre, ni hasard. Les chryzodes permettent d'aborder l'arithmétique sous un angle nouveau, particulièrement le nombre dans ses opérations simples, dans le domaine des congruences ou des suites. Un autre aspect important parait être l'utilisation du référentiel
circulaire qui permet d'envisager une géométrie des chryzodes
en complément de la géométrie analytique, en particulier
quand il s'agit de rendre compte d'un processus ou d'une transformation.
Au premier coup d'oeil, on comprend la puissance de représentation
du modèle: l'économie dans l'information contenue. L'analogie
avec l'idéal des mathématiques grecques dans sa recherche
d'alliance entre beauté et proportion est ici indéniable.
Achevons l'aspect mathématique du modèle en le reconnaissant
comme appartenant à la nouvelle branche inaugurée notamment
par Poincaré, Julia, Thom ou Moulin, et concernant le chaos, le
désordre, les catastrophes, les fractals, les relateurs arithmétiques.
Cette conception se rapproche incontestablement d'une nouvelle épistémologie
avec la considération de la réalité comme un possible
"construit" plutôt au lieu d'un "donné" reflétant une
réalité immuable. La création de modèles est
un des outils importants de ce mouvement et le système des chryzodes
semble être en mesure de favoriser des simulations quand il s'agit
de phénomènes de nature périodique ou ondulatoire. . Appendices
Définition Si le rapport R/r est une fraction qui sous sa forme irréductible est de la forme p/q (q différent de 1), alors l'épicycloïde est aussi une courbe algébrique et se compose de p branches égales." Historique "les astronomes de la grèce antique expliquaient les mouvements
rétrogrades des planètes en leur conférant un mouvement
uniforme suivant une circonférence (épicycle) dont le centre
se déplace sur une autre circonférence. la propriété
selon laquelle le point d'une circonférence roulant intérieurement
sur une circonférence immobile de rayon deux fois plus grand décrit
le diamètre de la circonférence immobile fut découverte
indépendamment par nassir eddin (milieu xiiiè siècle)
et nicolas copernic (début xviè siècle). Textes extraits de "aide mémoire de mathématiques supérieures", M Vygodsky, ed. de Moscou, 1973. . D-a-2-Méthode de diffraction en rayonnement polychromatiqueIl n'existe qu'une méthode de diffraction en rayonnement polychromatique
et elle s'adresse exclusivement aux monocristaux: c'est la méthode
de Laue. On emploie une anticathode de tungstène A excitée
sous une tension de 50 à 80 kilovolts. On dispose ainsi d'un spectre
continu compris entre 0,2 et 2 A. On obtient un faisceau approximativement
parallèle au moyen de deux trous de quelques dixièmes de
millimètres percés dans deux plaques de plomb montées
aux extrémités d'un tube métallique. Le faisceau tombe
sur le cristal et les taches de Laue se forment sur la surface sensible
S. Les distances de A à D1 et de D1 à D2 sont de l'ordre
de 4 ou 5 cm. Le cristal C est placé très près du
diaphragme D2. La distance CO, de C à S varie de 2 à 10 cm. Pour montrer le caractère polychromatique des diagrammes de
Laue, nous en avons réalisés en couleur avec l'artifice suivant. Textes extraits de: " principes de radio-cristallographie" de Jean
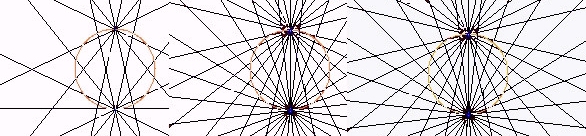
Barraud, Masson ed., 1960, p 84 à 87. . D-a-3- Détails d'une superposition de réseauxDans ce qui suit nous étudions deux cas de figure asymptotiques, soit : 1) Superposition de réseaux dans des modules multiples d'un
même nombre. 1) Superposition de réseaux dans des modules multiples d'un même nombre. Dans l'exemple ci-dessous chaque couche illustre un nombre croissant d'éléments en interaction.
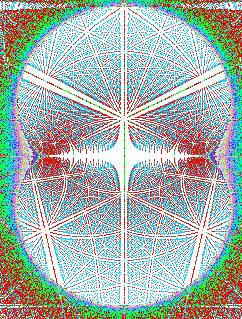
2) Superposition de réseaux dans des modules de valeurs consécutives.Avec un petit intervalle (ou pas) entre chaque nombre, les faisceaux harmoniques disparaissent laissant place à une cinématique de formes tourbillonnantes composées d'un enchevêtrement de moirages, courbes, cols, noeuds, foyers.
On peut bien sûr exprimer d'autres puissances que celles de 2
ou 3. Varier le type d'opération et le type de fonction amène
à découvrir une infinité de figures. Cette infinité
des topologies réalisables et les niveaux cybernétiques qu'on
y décèle aisément nécessiteraient une thèse
à eux seuls. En fait, bien des aspects sont encore à résoudre.
Résumons en disant que les chryzodes expriment graphiquement des
propriétés arithmétiques qu'on peut étendre
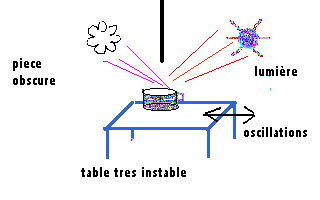
aux nombres réels par approximation. D-a-4 Miroir circulaire vibrantUn exemple simple permet d'approcher les phénomènes physiques générant des figures liées aux formes découvertes par les chryzodes.Posons sur un support instable un large récipient circulaire réfléchissant et contenant un peu de liquide . Soit par exemple une grande casserole en aluminium avec un peu d'eau à l'intérieur et posée sur une table branlante. Eclairons ce récipient par un faisceau lumineux de telle façon que se réfléchisse au plafond d'une pièce obscure les réfractions lumineuses provenant de la casserole. Au repos, nous observons dans les reflets un simple miroitement comme il s'en produit à la surface d'une étendue d'eau.
Parcourant verticalement et horizontalement la table des multiples congrus
à un nombre, les chryzodes relatent une cinématique de topologies
épi et hypocycloïdiques. Chacune de ces formes est elle-même
composée de tout un spectre de cycloïdes fractionnaires. Ces
différentes oscillations entre l'interne et l'externe selon des
processus d'expansion-implosion peuvent être résumées
la plupart du temps par le couple d'inverses : a * b = 1 mod m.
|
1 10 13 5 4 16 11 12 17 2 7 8 3 15 14 8 9 18 soit les couples verse-inverse: 2*10, 3*13, (4*5), (5*4), (6*16), etc. Dans un nouveau chryzode, nous représentons donc ces différents
couples au moyen de vecteurs reliant les termes de chaque couple. |
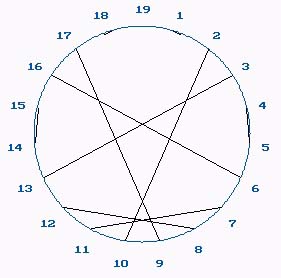 |
Ci dessous, nous avons representé les couples d'inverses des nombres 232 à 235.
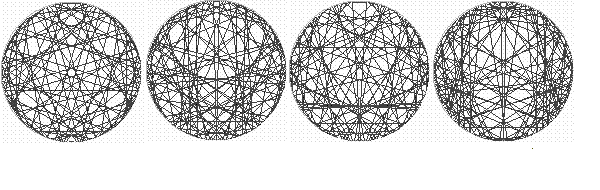
Voir ci-contre la superposition dans un même cercle des chryzodes identités des nombres de 5 à 50. |
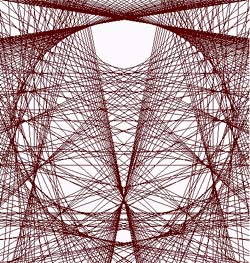 |
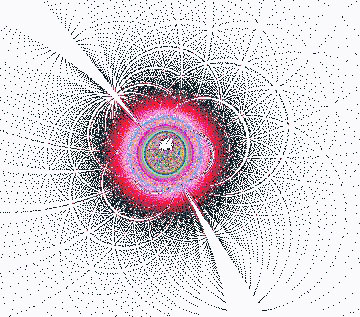
Disons, pour conclure, que ce type de nouvelle forme ressemble un
peu à un coquillage dans les premières étapes de sa
construction, mais que très rapidement cette forme s'estompe au
profit d'une topologie non classifiée à ce jour. |
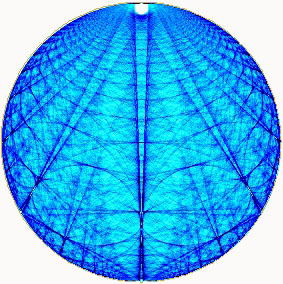 |
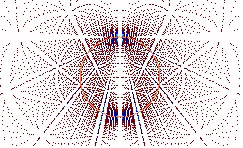
D-a-6 Comparaison entre la courbe de Helmoltz et le chryzode
Pour conclure, citons un intéressant parallèle entre la
position et l'intensité des pics d'inflexion intérieurs de
la superposition des polygones étoilés dans un chryzode (scindé
en deux) et la courbe de consonance de Helmoltz. Cette dernière
est établie à partir de la concordance harmonieuse entre
un son DO et un autre son produit par une corde musicale montant de ce
DO jusqu'au DO de l'octave supérieure.
|
 |
Conclusion de l'annexe D
Les chryzodes décrits dans cet exposé ne sont que les premières lettres d'un alphabet de la forme, et bien d'autres traitements structuraux sont applicables pour chaque aspect d'une résonance structurale. Dans la pratique de la vie, l'organisation des choses est bien plus subtile que toutes les rationalisations possibles (heureusement !). La vie modifie les modèles, les moules, à sa convenance, en respectant toutefois certaines contraintes. Pourtant, pour aussi simples que soient les chryzodes, ceux-ci ne sont pas à délaisser: ils possèdent de nombreuses analogies d'organisation par rapport à notre logique de perception et, d'autre part, on trouve dans la recherche neurophysiologique actuelle divers indices qui tendent à appuyer l'incidence d'une telle organisation au sein de notre cerveau. La similitude des décodages vectoriels ne doit pas nous échapper, d'autant que les chryzodes sont en eux-mêmes une voie logique de (dé)codage. Apparemment, le cortex visuel des singes exprime une prédilection d'analyse pour des angles espacés de 10 degrés. Dans une application chryzoïdique, nous pourrions dire que le relateur préféré du singe est un anneau chryzoïdal muni de 36 angles différents, soit une base exponentielle ( puissance de ... ) 37. Ceci n'est qu'une façon rudimentaire d'entrevoir des champs d'application plus succincts..
BIBLIOGRAPHIE de l'ANNEXE D
"le cerveau" ; Ed. Pour la Science, nov. 1979.
"la recherche", Laure Schachli, décembre 1991.
" principes de radio-cristallographie", Jean Barraud, Masson ed.,
1960, p 84 à 87.
"les nombres premiers " ; J. Itard : PUF.
"hypocycloïdes et epicycloïdes" ;J. Lemaire : Libr. Blanchard.
"théorie des nombres" ; E. Lucas : Librairie Albert Blanchard.
"aide mémoirede mathématiques sup." ; M. Vygodski :
Ed. Mir.
"aide mémoire de physique" ; B. Yavorski et A. Detlaf :Ed.
Mir.
.
BIBLIOGRAPHIE SUR LES CHRYZODES
"actes congrès MATh.
en. JEANS. 1996, Pierre Duchet ; ed MATh en JEANS, Paris
"eurêka",Helène Prost, décembre 1995, Bayard
Presse, Paris
"encyclopedia
of world problems & human potential ", Anthony Judge, 1994,
ed u.i.a., Bruxelles
"journées
nationales apmep 1993", Pierre Germain, Jean-Paul Sonntag,
ed. APMEP, Paris
"science en fête 1993", Corinne Rouiller, Pierre Germain,
Jean-Paul Sonntag, Ministère de la Recherche, Paris
"second european congress on systems science in prague- proceedings",
1993, ed. UES.-AFCET, Pierre Germain, Corinne Rouiller.
"u.a.t.i., n 1", Marcel
Locquin, 1993, ed. UNESCO,
Actes Congrès "MATh.
en. JEANS. 1993", Pierre Audin, ed MATh.en.JEANS, Paris
"actes
congrès international uitf 1992", Corinne Rouiller, Jean-Paul
Sonntag,
ed UITF, Paris
"actes colloque systema 1992", Pierre
Germain, Jean-Paul Sonntag, AFCET,
Paris
"programme
chryzode v.2 pour pc (windows)", Assoc. Résonances Transdisciplinaires (A.R.T.)
"introduction
aux chryzodes", Assoc. Résonances Transdisciplinaires (A.R.T.)
"Boulé
!", Bulletin de l'Assoc. Résonances Transdisciplinaires (A.R.T.)
"introduction à une cybernétique des formes" (épuisé),
Assoc. Résonances Transdisciplinaires