Chryzode
Un voyage en images dans la science des nombres (arithmétique)
A pictorial travel into arithmetic

Chryzodes en ligne

On réalise de superbes découvertes en combinant le cercle, la ligne et le point avec les chiffres des additions, des multiplications ou des divisions.

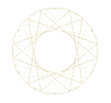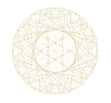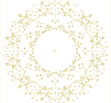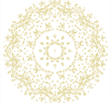
ex. 1 / multiplication par 3
dans un cercle partagé en 7 points equidistants

On représente la multiplication par 3 en reliant par des lignes chaque nombre à son triple :
Sur le cercle, du point 1 nous traçons donc une droite qui va au point 3, puis une autre qui va de 3 à 2, puis de 2 à 6, etc.

1 * 3 = 3; nous relions par un trait 1 et 3
2 * 3 = 6; nous relions par un trait 2 et 6
3 * 3 = 9; nous relions par un trait 3 et 2
(car 9 - 7 = 2 dans un cercle de 7 points)

EXEMPLE 1 /
MULTIPLICATION PAR 3 DANS LE NOMBRE 7

Comme exemple, étudions la multiplication par trois au moyen de la progression des triples soit: 1, 3, 9, 27, etc. et dessinons celle-ci en nous aidant d'une circonférence où nous définissons N = 7 points équidistants numérotés de 1 à N.

Il suffit alors de relier simplement par des droites les points sur la circonférence selon l'ordre correspondant à la valeur des termes de la suite.

Evidemment la progression des triples théoriquement infinie, sera ici limitée par le nombre des éléments de N. Aussi, chaque fois que la valeur d'un terme de la suite est supérieure à la valeur de N, nous retranchons autant de fois que nécessaire la valeur de N à celle du terme de la suite. De la même façon nous comptons les heures où la 26ème heure équivaut à 2 heures.

En arithmétique on dit que les termes sont congrus au nombre N. De cette façon, la progression: 1, 3, 9, 27,etc. se transforme en une suite périodique de 6 termes: 1, 3, 2, 6, 4, 5, 1, etc..(9 = 9-7 = 2).

Avez vous bien compris ?

EXEMPLE 2 / MULTIPLICATION PAR 3 DANS LE NOMBRE 61

En utilisant un nombre plus grand d'éléments sur le cercle, nous obtiendrons une meilleure définition graphique. Nous y observons que les droites sont tangentes à une courbe en forme de huit appelée néphroïde.

ex. 2 / multiplication par 3 dans un cercle partagé en 61 points equidistants